这个答案要从一个题开始。
基本上所有的语言都提供了一个random方法来获取一个随机数，以js为例， Math.random() 将返回0到1之间的任意值。这个方法所有的值都是等概率的，从概率论角度来说，即该方法的概率密度函数为常量，为：p(x) = 1, x∈(0,1)
如果将随机变量做一次处理，例如平方，那么它的概率分布将会怎么样。得到下题：
如果x为(0,1)上的随机变量，且概率密度函数为p(x) = 1, x∈(0,1)，求y=x^2的概率密度函数。
这个题啊，其实很简单，如果是当初大一的时候还在上概率论的课，两分钟就解出来了。不过虽然很久没接触概率论，花点时间还是能解出来的。
这里还有个坑。如果任意y都对应的唯一确定的x，那么得到这个y值的概率应该和这个x的概率是相同的，而获取任意x的概率处处相等，所以y的概率分布和x是相同的。 错！如果x与y是离散的随机变量，那么这个结论是正确的，即y的概率与x的概率分布是相同的。可惜，这里的x是连续的，不能这里来计算。
由于x是连续的，所以没有办法得到某个确定的x的值的概率，比如说x取到0.5的概率是多少，这个是没有答案的，我们只能得到x取值为 0.49到0.51之间的概率是多少，这个的答案为其概率密度函数的在0.49与0.51上的定积分。擦，出现积分了。还好这个是常量函数。
这里也是个坑，因为之后会遇到其他的积分。如果是大一的时候还在上微积分的课程，一般简单的函数的积分还是能秒秒钟算出来的，复杂一点的分步积分花个几分钟也能求出来，可惜现在基本已经废了。然后去复习了一下。
很明显y∈(0.49,0.51)的概率，就是x^2∈(0.49,0.51)的概率，即x∈(√0.49,√0.51)的概率，即 √0.51- √0.49。
经过上上面的思考，可以求得任意区间y的概率分布。得到 P(y1<y<y2) = √y2 - √y1
设y的概率密度函数为p(y)，由于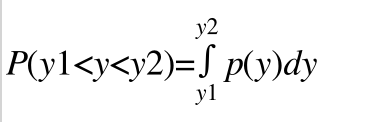
,即 
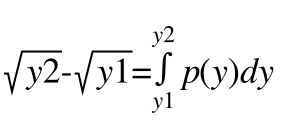; 很显然，
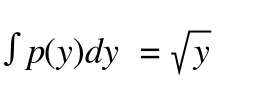， 所以可以求得y概率密度函数，即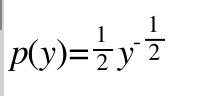 
复杂了一点，于是得到了最终的结果，y的概率密度函数，然后开始写一段代码验证一下.
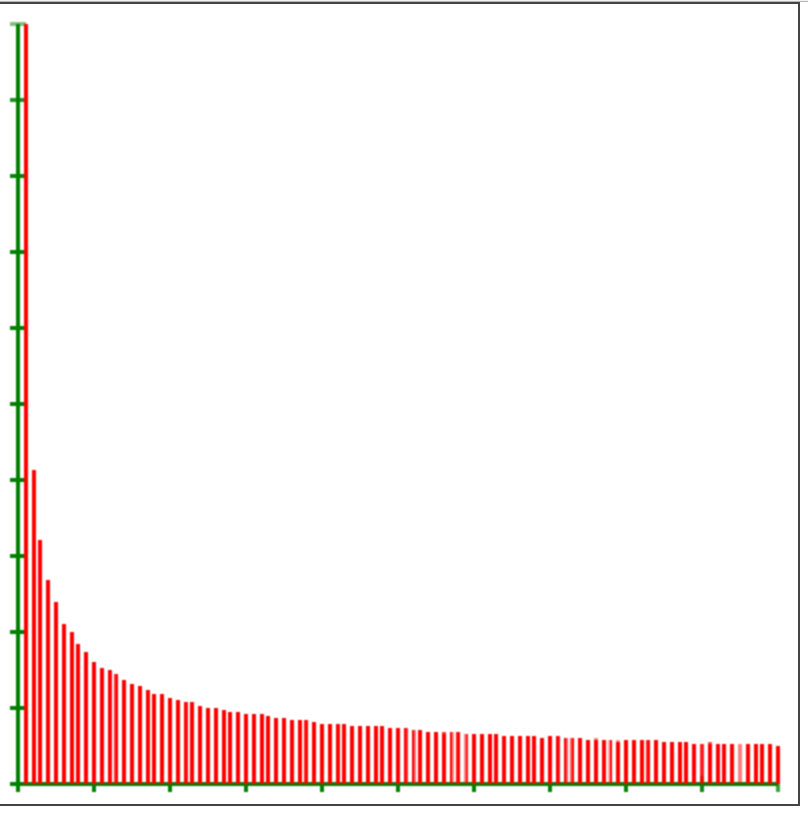
实验的结果如下图，实验次数为1000000，以0.01为统计最小单位:
然后画出函数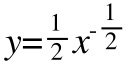
的图像，如下图，
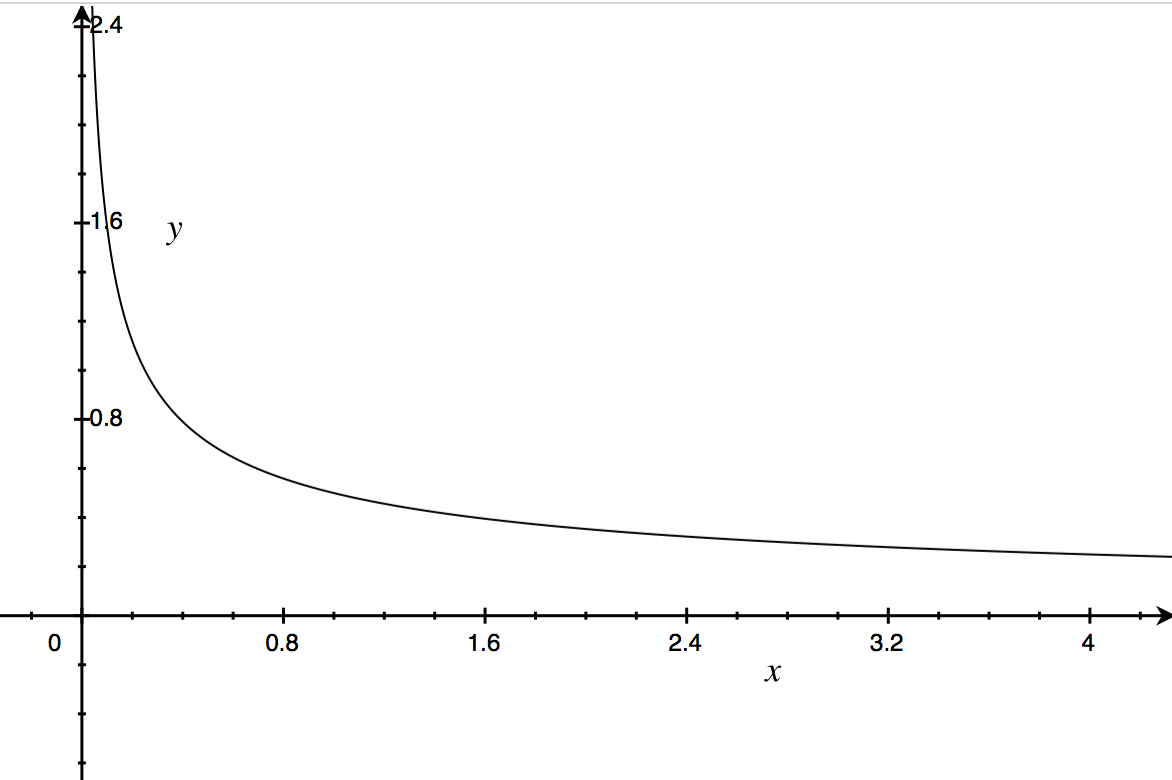
可以看出来，两图基本一致，看来没什么问题。
然后得出一个结论 ： p(y) = g’(y)，其中 g(y)为y关于x的反函数
简单的来说就是，如果x为随机变量，而且y = f(x)，那么y概率密度函数为 f(x)反函数的导函数。
那如果反过来呢，已知一种概率分布，求积分，再求反函数，得到的f(x)是否是正确的。证明就不证了，直接上测试。
这个测试的例子是以前段时间某次抽奖活动为原型，也是本篇文章主题的起源点，具体数据纯属胡扯。
抽奖要求：后百分之五十的抽到概率为前百分之五十的概率的两倍。
构造一个概率分布函数，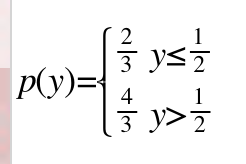
，这是一个分段函数，
求不定积分得到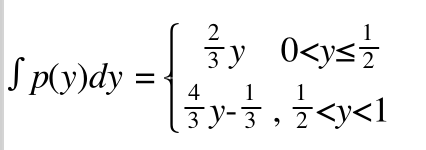 
求反函数得到最终结果，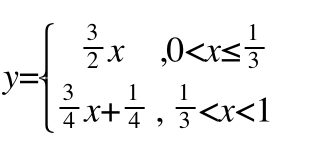 
迫不及待验证一下。
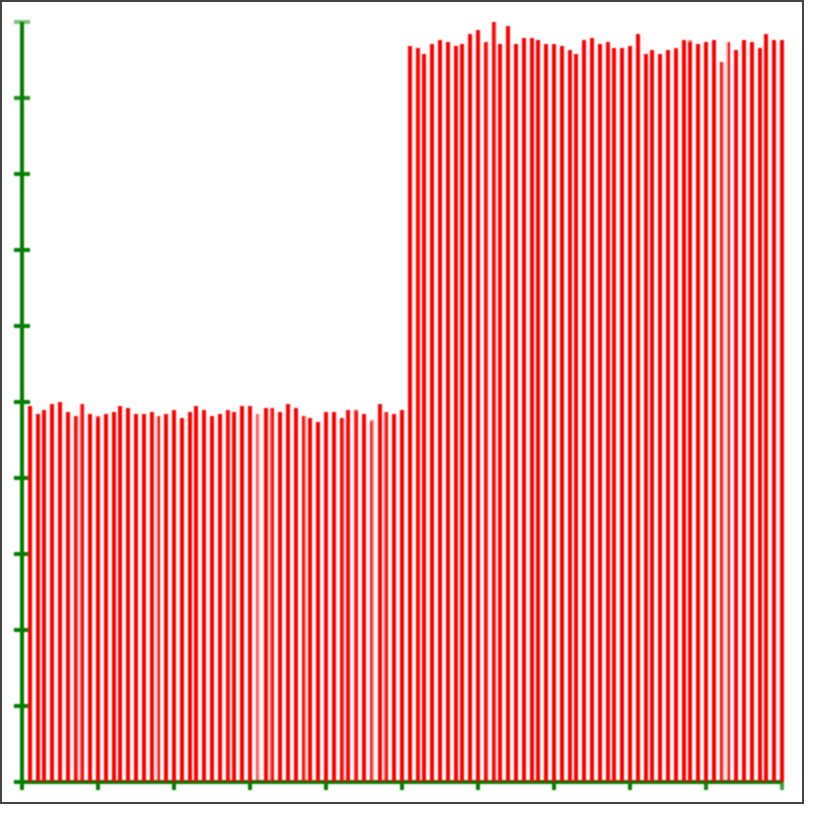
卧槽 简直完美。
于是就从数学上得到了一种可以构造任意分布的随机变量的方法。函数调用非常简单，只需要将Math.random()的到的数据进行二次处理即可，麻烦的地方在于根据要求构造概率分布函数，以及对这个函数求不定积分。例如，构造一个正态分布的随机变量就会比较麻烦，因为正态分布积分有点点难算
很久没有接触概率论和微积分了，中间有很多疏漏。
再来一个，令 f(x) = √(2x); 得到下图，求解得到 p(y) = y， 也是一致的，perfect。
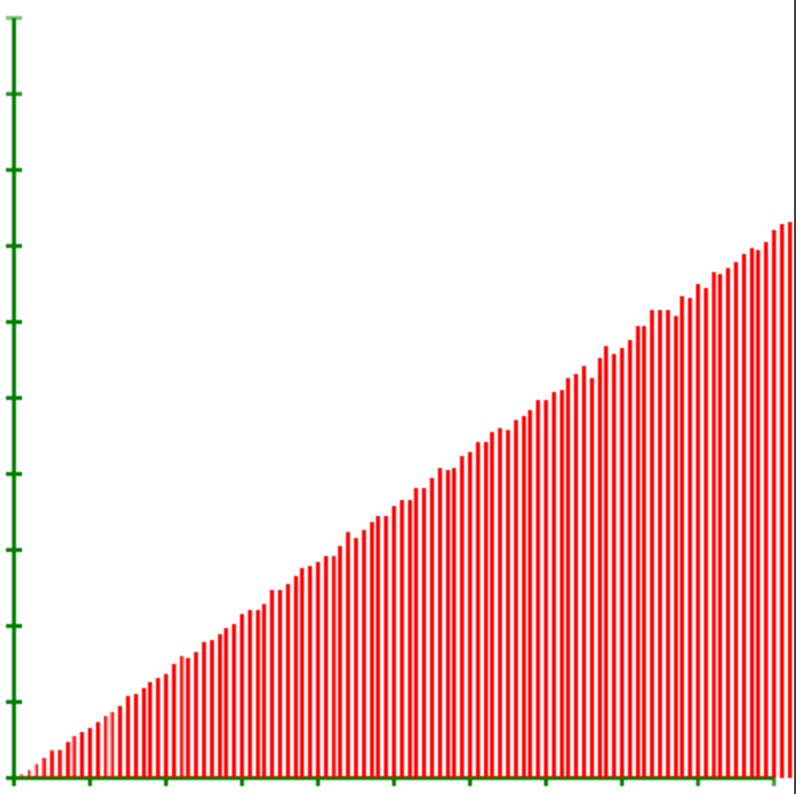
所有的代码在这里, https://github.com/thesadabc/blog-demo/tree/master/random,