使用JS的进行GPU计算

前端是可以接触到GPU的于是也是可以使用GPU的计算能力的对于我这种没有很深入的GPU运算了解的程序员来说完全从底层开始怕是也不太可能好在已经有大神把相关的内容以及封装成库了 gpu.js 于是本文的初识的意思就是就从这个库开始首先说明这个库其实也还在开发当中的也没有一个很稳定的正式版所以很多功能都是有欠缺的但是了解个GPU计算是啥来说绰绰有余了

因为js是单线程的所以并不适合处理CPU密集型的程序但是GPU是有非常高的并行线程数所以GPU计算的基本思想就是把计算任务分拆成N多个线程任务每个线程返回一个结果然后吧每个线程的结果再汇总这个基本的思路不管是哪平台上的应该都是一样的

啥是线程的概念咱先直接看一段代码来先感受一下

const gpu = new GPU();
const myFunc = gpu.createKernel(function() {
    return this.thread.x;
}, { output: { x: 100 } });

myFunc();  // [0,1,2,3,...98,99]

每个线程都会执行这个传入的函数具体起多少个线程有参数output决定可以有x,y,z三个维度上面这个例子只取了x方向上数量100个

在函数里this.thread.x可以获取到当前执行这个函数的线程x维度上的地址如果有多个方向的话还有类似this.thread.y和this.thread.z的

函数接受的参数为外部调用的时候传入的参数函数返回的值为当前线程返回的值所有线程按照各个维度上的位置向最外面返回一个最终的数组就是上面那个执行的效果每个线程直接返回了线程在x维度上的位置最终吧所有线程按照维度的顺序合并起来如果有两个维度最终的值就是个二维数组同理三个维度也是

要注意的是这个执行的函数最终会被库转化进入到GPU中执行所以所有外部js的参数和函数还有该函数里的语句语法是有限制的具体的解决方法可以参考文档有向内部传入数据的方法

矩阵乘法实现

说了这么多咱来写一个实际有用的东西矩阵相乘 C=AB 为了方便起见 A和B都是相同大小的方块矩阵

矩阵的乘法咱就不回顾了只提一个非常关键的地方就是关于矩阵C中 C(i,j)的值

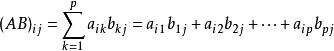
multiply

这个很关键先吧这句翻译成程序语句

let dimensions = 100; // 假设长度为100
function getValue(ma, mb, x, y) {
    let sum = 0;
    for (let i = 0; i < dimensions; i++) {
        sum += ma[x][i] * mb[i][y];
    }
    return sum;
}

于是开始写

const matrixMultiplyGPU = new GPU().createKernel(function(a, b) {
        // 计算每个坐标的值, 注意这里的x,y顺序是反的
        return getValue(a, b, this.thread.y, this.thread.x);  
    }).setOutput({ x: dimensions, y: dimensions })
    .setHardcodeConstants(true)
    .setConstants({ dimensions }) // 添加外部变量
    .setLoopMaxIterations(1000)
    .setFunctions([getValue]); // 添加外部函数, 添加外部函数的时候有非常多bug

这里注意一点线程在两个维度上的坐标顺序与结果的顺序是反的比如线程在两个维度上是[i, j]那么在最终的结果里的位置是[j, i] 不知道这里是为啥要这样做可能和GPU的原理有关

然后咱们随机构造矩阵然后开始计算

function createMatrix(dims, fn) {
    let matrix = [];
    for (let i = 0; i < dims; i++) {
        matrix[i] = [];
        for (let j = 0; j < dims; j++) {
            matrix[i][j] = fn(i, j);
        }
    }
    return matrix;
}
const randomMatrix = createMatrix(dimensions, () => Math.floor(Math.random() * 50));


const retMatrix = matrixMultiplyGPU(randomMatrix, randomMatrix);

哈哈哈为了方便起见两个相同的矩阵相乘好了拿出笔和纸用个两三个维度的值验证了一下发现没有问题但是这个效率和CPU的相比有多大的优势呢

和CPU比

然后咱们利用上面的式子写一个matrixMultiplyCPU吧因为有上面的铺垫所以这个就非常简单了

1
2
3

const matrixMultiplyCPU = function(a, b) {
    return createMatrix(dimensions, getValue.bind(null, a, b));
}

验证的也很简单直接看一下运行时间对比就可以了

console.log("dimensions", dimensions)

console.time("matrixMultiplyGPU");
matrixMultiplyGPU(randomMatrix, randomMatrix);
console.timeEnd("matrixMultiplyGPU");

console.time("matrixMultiplyCPU");
matrixMultiplyCPU(randomMatrix, randomMatrix);
console.timeEnd("matrixMultiplyCPU");

![time1](//blog-cdn.xjp.in/2017/10/Screen Shot 2017-10-22 at 21.15.22.png)

电脑配置是

CPU - 2.6 GHz Intel Core i5
GPU - Intel Iris 1536 MB
Browser - Chrome Version 61.0.3163.100 (64-bit)

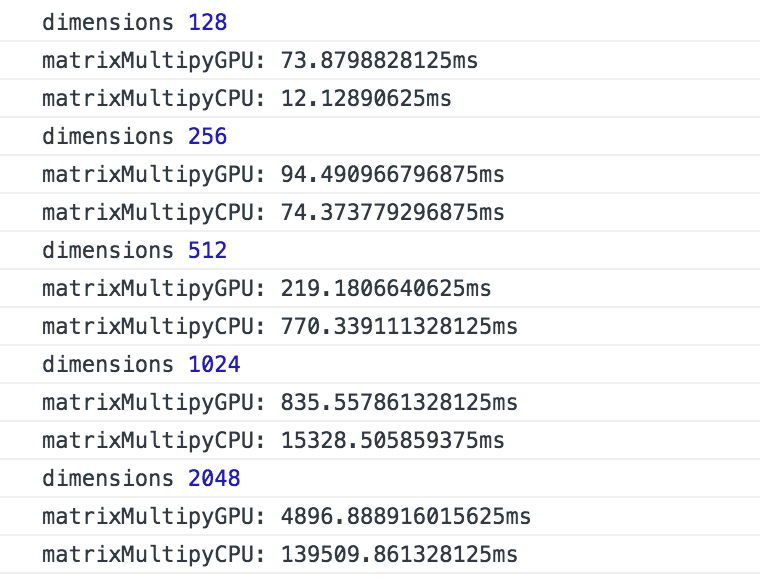
然后我再看下另外的结果

time2

后面这个的配置就略高一些所以整体的数据比上面的好一些但是其中有个数据出了点偏差具体啥原因也不知道重新跑了之后结果也没大问题

CPU - 3.2 GHz Intel Core i5-6500
GPU - NVIDIA GeForce GTX 1060 3GB
Browser - Chrome Version 61.0.3163.100 (64-bit)

从上面的数据来看当矩阵维度较小的时候CPU的耗时比较短因为当数据量少的时候时间主要花费在将数据传输上从内存传到显存当数据量大了之后计算时间开始增大 GPU才开始显现出优势

由于显存与内存本据存取上的区别上述的代码也有非常大的优化空间上述例子中GPU最大达到80倍的效率应该还是可以继续增加的

当然 GPU的维度也不是越大越好实测维度过大了之后计算还是会奔溃的具体最佳的维度大小应该和各个GPU自己有关吧

代码

演示